相信各位童鞋上学的时候都有想过「为什么要学这种以后用不到的科目呢?」，其实每一个科目、每一个理论说不定都会在意想不到的时候派上用场!最近有位日本网友教导大家将简单的数学几何套用在《Pokemon Go》能够有效提升捕捉宝可梦的效率，如此一来就有理由劝孩子好好读书了吧……
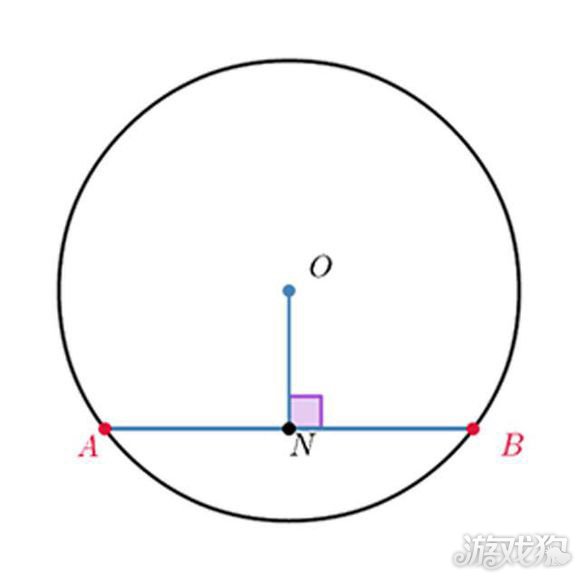
弦的中垂线必通过圆心——
差不多在初中的数学科目就教过圆上任一弦的中垂线(垂直平分线)必通过圆心，大家虽然学过这个定理但是曾经应用在现实生活吗?对于《Pokemon Go》的玩家而言终于有机会实践了……
使用雷达寻找宝可梦——
《Pokemon Go》的雷达会显示玩家周围的宝可梦，没捕捉过的则只会看到影子轮廓，由于雷达是侦测一个圆型范围而没有显示方位因此不容易立刻判断宝可梦的位置，日本网友MAEDA Katsuyuki就将运用几何定理的寻宝法做成一张图解引发热烈讨论!
如何使用几何定里寻宝的图解——
下面就一个一个步骤解说吧……
寻找宝可梦的踪迹在哪里消失：
假设玩家一开始在S点发现宝可梦的踪迹，首先就要赶紧找到影子消失的地点A，这个时候就可以确定A点位在宝可梦被雷达侦测的圆形范围边缘，也就是圆周之上了!
寻找第二个消失的地点：
找到A点以后，接着转弯再次进入雷达侦测的范围之内，然后直直走到下一个影子消失的地点B，这个AB连线就是以宝可梦为中心的圆形上的一条弦了!
回头寻找中垂线路径!
最后就是从B点回头走到AB连线的中点，沿着通过这一点并且与AB连线垂直的路径寻找就可以发现宝可梦了!当然目标也可能会在图示的另外一侧，玩家要是发现沿着中垂线走着走着影子竟然消失就是走反啰!
运用简单的几何数学成功找到宝可梦!
平常会时不时有说「干嘛要学这种以后用不到的科目呢?」，从这个案例可以了解学会的知识永远不知道会在什么时候突然派上用场啊!
但是这对与10岁左右的童鞋来说可能困难了一点......但正因这样才有理由叫小孩子好好读书!